
Teilbarkeitsregeln
Manchen
Zahlen "sieht man unmittelbar an", ob sie durch
eine andere Zahl teilbar sind. Unterscheidungskriterien sind z. B. Endziffern
und Quersummen.
"Endziffernregeln"
Die Schreibfigur " zn zn-1 zn-2 ... z2 z1 z0 " nennt man Zifferndarstellung einer natürlichen Zahl, wobei für die Ziffern zi gilt: zi  {0, 1, 2, ..., 9}
und zn
{0, 1, 2, ..., 9}
und zn  0.
0.
(Die einzelnen Ziffern sind ohne Malpunkte aneinandergereiht.)
Beispiel:
Zifferndarstellung der Zahl Viertausendsechshundertsiebenunddreißig:
4637 mit z3 = 4, z2 = 6, z1 = 3, z0 = 7.
Im Dezimalsystem bedeutet die Zifferndarstellung zn zn-1 zn-2 ... z2 z1 z0:
a = zn · 10n + zn-1 · 10n-1 + zn-2· 10n-2 + ... + z2 · 102 + z1 · 101 + z0 · 100.
Wichtig für die weiteren Überlegungen sind folgende Identitäten:
a = zn · 10n + zn-1 · 10n-1 + zn-2· 10n-2 + ... + z2 · 102 + z1 · 101 + z0 · 100
a = 10· (zn · 10n-1 + zn-1· 10n-2 + zn-2· 10n-3 + ... + z2 · 101 + z1 · 100) + z0
a = 100 · (zn · 10n-2 + zn-1· 10n-3 + zn-2· 10n-4 + ... + z3 · 101 + z2 · 100 ) + z1z0
a = 1000 · (zn · 10n-3 + zn-1· 10n-4 + zn-2· 10n-5 + ... + z4 · 101 + z3 · 100 ) + z2z1z0

Teilbarkeitsprüfung
(funktioniert nur bei installiertem OpenOffice)
| Satz 7: "Endziffernregeln" Sei a  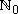 und zn zn-1 zn-2 ... z2 z1 z0 die Zifferndarstellung der natürlichen Zahl a. und zn zn-1 zn-2 ... z2 z1 z0 die Zifferndarstellung der natürlichen Zahl a. |
| a) | Wenn 2  z0, z0,dann gilt: 2  a. a. |
| b) | Wenn 4  z1z0, z1z0,dann gilt: 4  a. a. |

| c) | Wenn 5  z0, z0,dann gilt: 5  a. a. |
| d) | Wenn 8  z2z1z0, z2z1z0,dann gilt: 8  a. a. |
| e) | Wenn 10  z0, z0,dann gilt: 10  a. a. |
| f) | Wenn 25  z1z0, z1z0,dann gilt: 25  a. a. |
| g) | Wenn 100  z1z0, z1z0,dann gilt: 100  a. a. |
| Definition 3: "Quersumme" Sei zn zn-1 zn-2 ... z2 z1 z0 die Zifferndarstellung der natürlichen Zahl a. Dann nennt man Q(a): = zn + zn-1 + zn-2 + ... + z2 + z1 + z0 die Quersumme von a. |
Wenn man die Ziffern einer natürlichen Zahl a abwechselnd addiert
und subtrahiert, nennt man das Ergebnis die alternierende Quersumme
QA(a) von a.
QA(a) =
zn - zn-1 + zn-2 - ...  z2
z2  z1
z1  z0.
z0.
Beispiel: a = 1324.
Q(a) = 1 + 3 + 2 + 4 = 10
QA(a) = 1 – 3 + 2 – 4 = -4
| Satz 8: "Quersummenregeln" |
| a) | Sei a  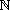 und zn + zn-1 + zn-2 + ... + z2 + z1 + z0 die Quersumme Q(a) von a. und zn + zn-1 + zn-2 + ... + z2 + z1 + z0 die Quersumme Q(a) von a. |
Wenn 9  Q(a), Q(a),dann gilt: 9  a. a. |

| b) | Sei a  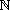 und zn + zn-1 + zn-2 + ... + z2 + z1 + z0 die Quersumme Q(a) von a. und zn + zn-1 + zn-2 + ... + z2 + z1 + z0 die Quersumme Q(a) von a. |
Wenn 3  Q(a), Q(a),dann gilt: 3  a. a. |
| Satz 9: "Teilbarkeit durch 11" Sei a  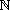 und
zn - zn-1 + zn-2 - ... und
zn - zn-1 + zn-2 - ...  z2 z2  z1 z1  z0 die alternierende Quersumme QA(a) von a. z0 die alternierende Quersumme QA(a) von a. Wenn 11  QA(a), QA(a),dann gilt: 11  a. a. |


Übung:
Formulieren Sie eine Teilbarkeitsregel für die Zahl 15.