Vorbemerkung:
Einer der grundlegenden Begriffe in der Mathematik ist der Begriff der „Relation“. Eine Relation drückt Beziehungen zwischen mathematischen Objekten wie Zahlen oder Mengen aus.
| Beispiele: | mathematische Ausdrücke, wie | "...ist kleiner als...." |
| "...ist parallel zu..." | ||
| aber auch Alltagsbeziehungen, wie | "...ist Sohn von..." | |
| "...sind Eltern von..." | ||
| beschreiben Relationen zwischen Objekten. | ||
| Definition 1 Seien A, B nichtleere Mengen. Dann nennt man A x B := { (a,b) 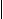 a a  A und b A und b  B } das Kreuzprodukt oder kartesisches Produkt von A und B. B } das Kreuzprodukt oder kartesisches Produkt von A und B. (a,b) nennt man geordnetes Paar. |
| Beispiel: | Seien
A = { x , y } , B = { 5 ,0 , 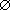 } } Dann ist A x B = { (x , 5) , (x , 0) , (x , 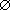 ) , (y , 5) , (y , 0) , (y , ) , (y , 5) , (y , 0) , (y , 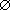 ) } ) } |

Begründen sie, warum im eben genannten Beispiel (5 , x) oder (x , y) nicht Elemente von A x B sind.
| Definition 2 Eine Menge R nennt man zweistellige Relation zwischen A und B genau dann, wenn R eine Teilmenge des kartesischen Produkts A x B ist. Anmerkung: Jede Teilmenge von A x B (also auch ganz A x B und auch die leere Menge) ist (nach Definition) eine Relation. Damit ist noch keine Aussage darüber gemacht, ob diese auch sinnvoll ist. Schreibweise: Statt (x , y)  R oder R (x , y) schreibt man auch x R y . R oder R (x , y) schreibt man auch x R y . |
| Beispiel: | Sei A:={a,b,c}, sei B:={v,w,x} Dann sind R1 = { (a,w) } oder R2 = { (b,v), (b,x), (a,v), (c,v) } Relationen. Es ist aber nicht notwendig zu wissen, welche Vorschrift diese Relationen beschreibt. Gegenbeispiel: R3 = { (a,v,w)} oder R4 = { (a,v) , (w,c)} beschreiben hier keine Relationen. |
| Definition 3 Die Menge D(R) := { x 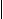 es gibt ein y mit (x,y) es gibt ein y mit (x,y)  R } nennt man Definitionsbereich von R, R } nennt man Definitionsbereich von R, die Menge W(R) := { y 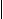 es gibt ein x mit (x,y) es gibt ein x mit (x,y)  R } nennt man Wertebereich von R. R } nennt man Wertebereich von R. |
Seien A = { 2 , 3 , 4 } , B = { 6 , 7 , 9 }
Wir betrachten die Relation “…ist Teiler von…” in A x B.
Aus der gesamten Menge der geordneten Paare A x B (siehe Definition oben) ergeben beim Einsetzen (2 , 6) , (3 , 6) , (3 , 9) wahre Aussagen bezüglich unserer Relation.
D(R) = { 2 , 3 } , W(R) = { 6 , 9 }
R = { (2 , 6) , (3 , 6) , (3 , 9) } ( = { (x , y)
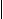 x
x  y mit x
y mit x  A und y
A und y  B } )
B } )Um Relationen zu veranschaulichen, bedient man sich u.a. folgender Darstellungen:
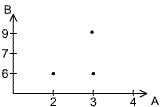 Graph |
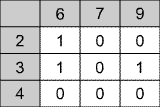 (0,1) Matrix |
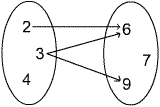 Pfeildiagramm |

Bei Relationen interessiert man sich für spezielle Eigenschaften, so zum Beispiel, ob Elemente zu sich selbst in Beziehung stehen.
Die Relation "…ist Teiler von.." hat diese Eigenschaft, denn jede Zahl ist Teiler von sich selbst. Ist dies der Fall, so sagt man die Relation ist reflexiv.
| Definition 4 R nennt man reflexiv (in M) genau dann, wenn x R x für jedes x  M, also wenn jedes x aus der Menge M zu sich selbst in Relation steht. M, also wenn jedes x aus der Menge M zu sich selbst in Relation steht. |
| Beispiele: | a) |  ("…ist Teiler von..") ist reflexiv in ("…ist Teiler von..") ist reflexiv in 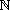 , denn für jedes n , denn für jedes n  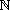 gilt: n gilt: n  n. n. |
| b) | ≤ ist reflexiv in 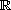 , denn x ≤ x für jedes x , denn x ≤ x für jedes x  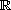 . . |
|
| c) | < ist nicht reflexiv, denn für kein x  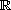 gilt x < x. gilt x < x. |
| Definition 5 R nennt man symmetrisch (in M) genau dann, wenn für alle (x , y)  M x M gilt: M x M gilt: Wenn x R y wahr ist, dann folgt daraus y R x, also falls x in Relation zu y steht, so auch y in Relation zu x. |
| Definition 6 R nennt man transitiv (in M) genau dann, wenn für alle (x,y,z)  M gilt: M gilt: Aus x R y und y R z folgt x R z, also wenn x in Relation zu y steht und y in Relation zu z, dann folgt daraus, dass auch x in Relation zu z steht. |

In welchem Spezialfall ist die Relation
 ("…ist Teilmenge von…") symmetrisch?
("…ist Teilmenge von…") symmetrisch?Ist die Relation
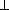 symmetrisch?
symmetrisch?Ist die Relation
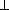 reflexiv?
reflexiv?Anmerkung:
Bei der Reflexivität handelt es sich um eine Aussage, die besagt, dass jedes Element der betrachteten Menge in Relation zu sich selbst steht.
Bei "der Symmetrie" dagegen wird nicht ausgesagt, dass x R y und y R x, sondern "nur": falls x R y dann auch y R x.
Analoges gilt für die Transitivität.
| Definition 7 Eine Relation, die reflexiv, symmetrisch und transitiv ist, nennt man Äquivalenzrelation. |
| Beispiel: | Sei M die Menge aller geometrischen Figuren. Sei ~ die Relation "…ist kongruent zu…" ~ ist eine Äquivalenzrelation, denn für x, y, z  M gilt: M gilt: |
|
| 1. | Reflexivität: x ~ x für jedes x  M M |
|
| 2. | Symmetrie: Wenn x ~ y dann folgt daraus y ~ x | |
| 3. | Transitivität: Wenn x ~ y und y ~ z, dann gilt x ~ z | |

Untersuche, ob die Relation R = "…ist Bruder von…" über der Menge {Tick, Trick, Track} eine Äquivalenzrelation ist.
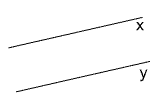
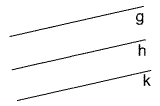
 B =
B =