
Alle natürlichen Zahlen
kann man durch wiederholtes Addieren der Zahl 1 erzeugen.
Ein Problem der Arithmetik ist, ob und wie man natürliche Zahlen
auch multiplikativ erzeugen kann.
 Primzahltest |
 Primzahltest (funktioniert nur bei installiertem OpenOffice) |
| Definition 1: "Primzahl"
Eine Zahl
a |
Beispiel: T(7) = {1, 7}, also |T(7)| = 2, also ist 7 eine Primzahl.
| Satz 1: "Satz von Euklid"
Es gibt unendlich viele Primzahlen. |

| Satz 2: "Primzahllücken" Wenn
n |
 Primzahlfunktion |
 Primzahllücken |

7! + 2 = 5042; 7! + 5 = 5045
7! + 3 = 5043; 7! + 6 = 5046
7! + 4 = 5044; 7! + 7 = 5047

Übung:
1. Zeigen Sie mit Hilfe der Definition, dass weder 1 noch 0 Primzahlen
sind.
2. Finden Sie 10 aufeinanderfolgende Zahlen, die nicht prim sind.

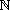 nennt man Primzahl, wenn |T(a)| = 2.
nennt man Primzahl, wenn |T(a)| = 2.