Das Komplement einer Menge
| Definition 4: "Komplement" Sei M eine Grundmenge und A  M.
M.Die Menge aller Elemente, die zu M aber nicht zu A gehören, nennt man Komplement von A bezüglich M. Formal: 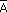 = { x = { x  M M 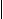 x x  A }. A }. |
| Beispiel: | M = {1, 2, 3, 4, 5, 6} und A = {1, 2, 5} dann gilt: 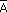 = {3, 4, 6 } = {3, 4, 6 } |
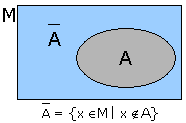
| Satz 5: "Doppelkomplement" Wenn
A eine Menge ist, |

| Beispiel: | M = {1, 2, 3, 4, 5} und A = {2, 3, 4} | |
| dann gilt: | 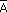 = { 1, 5 } = { 1, 5 }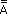 = { 2, 3, 4 } = { 2, 3, 4 }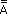 = A = A |
|
| Satz 6: "Komplement und Teilmenge"
Seien A und B Mengen. |

Definition 5: "Mengendifferenz" Seien A und B Mengen. |
| Beispiel: | A = {1, 2, 3, 4, 5} und B = {3, 5, 7, 8, 9} |
| dann gilt: B \ A = {7, 8, 9} |
| Satz 7: "Mengendifferenz" | |
| a) | Wenn A eine Menge ist, dann ist die Mengendifferenz von A in A die leere Menge. Formal: A \ A = 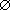 . . |

| b) | Wenn A eine Menge ist, dann ist die Mengendifferenz der leeren Menge in A die Menge A selbst. Formal: A \ 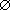 = A.
= A. |


Übung:
Stellen Sie verschiedene Möglichkeiten zu
folgender Situation graphisch dar: "A ist keine Teilmenge
des Komplements von B."
Mögliche Lösungen