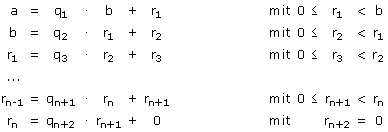Euklidischer Algorithmus
Der Euklidische Algorithmus ist ein Verfahren, den ggT zu bestimmen,
ohne auf die Primfaktorzerlegung zurückzugreifen.
Zunächst müssen noch zwei Sätze bewiesen werden, um den
Beweis zum Euklidischen Algorithmus vorzubereiten.
 Primfaktorzerlegung / Euklidscher Algorithmus |
 Euklidscher Algorithmus (funktioniert nur bei installiertem OpenOffice) |
| Satz 4: "Division mit Rest" Seien
a, b |

| Beispiel: | a = 29, b = 7 |
| 29 = 4 · 7 + 1 | |
| q = 4, r = 1 |
| Satz 5: "Teiler-Schnittmenge" Seien
a, b |

| Beispiel: | a = 16, b = 6, also a = 2 · b + 4 |
T(16)  T(6) = {1, 2} T(6) = {1, 2} |
|
T(6)  T(4) = {1, 2} T(4) = {1, 2} |
|
Also gilt: T(16)  T(6) = T(6) T(6) = T(6)  T(4) T(4) |
Da T(a)
 T(b) = T(b)
T(b) = T(b)  T(r), muss für a > b gelten:
T(r), muss für a > b gelten:ggT(a,b) = ggT (b,r) weil die Teilermengen gleich sind und somit der ggT(a,b) auch der ggT(b,r) ist.
| Satz 6: "Der Euklidische Algorithmus" Wenn a, b  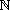 mit a > b sind, mit a > b sind,dann gibt es qi, ri  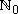 und ein n und ein n  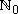 , so dass gilt: , so dass gilt:
|

| Beispiel: | a = 164, b = 44 |
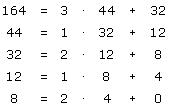 |
|
| ggT(164,44) = 4 |

Übung:
Ermitteln Sie mit Hilfe des Euklidischen Algorithmus
den ggT von 781 und 638.