Wir betrachten die Definition des Lagrange-Interpolationspolynoms:

Sei  eine Abbildung, seien  paarweise verschiedene reelle Zahlen.
Dann heißt



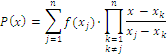
das zu  gehörige Lagrange-Interpolationspolynom.

Um ein erstes Verständnis zu gewinnen, reduzieren wir die Anzahl der reellen Argumente auf 2 und schreiben das Polynom einmal ohne Summen- und Produktzeichen auf.



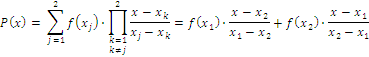
Wir erhalten ein Polynom vom Grad  und untersuchen die Funktionswerte von  an  bzw. .





Das Lagrange-Polynom nimmt also für  bzw.  jeweils den Funktionswert  bzw.  an.
Aus der Schule ist bekannt, dass durch zwei Punkte des  mit verschiedenen - Werten genau eine Polynomfunktion vom Grad  konstruiert werden kann, ebenso dass durch drei Punkte mit paarweise verschiedenen -Werten genau eine höchstens quadratische Polynomfunktion verläuft. Damals wurde mit 3 Gleichungen mit 3 Unbekannten gearbeitet und mehr oder minder mühsam die Koeffizienten berechnet. Demgegenüber bietet das Lagrange-Polynom den Vorteil, direkt durch Einsetzen aus  und   die Koeffizienten berechnen zu können.


Wie funktioniert Lagrange nun genau? Wir betrachten das Verfahren erneut, jetzt mit .

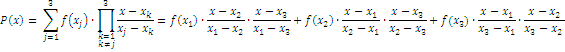
Setzen wir nun wieder -Werte in  ein, so ergibt sich bei dem  -ten Summanden genau  der Funktionswert , bei allen anderen Summanden jedoch die Null, erzwungen durch den Faktor . Somit wird das Konstruktionsprinzip dieser Formel einsichtig und die Formel selbst verliert an Schrecken.

Präsenzaufgabe:

Konstruieren Sie das Lagrange Polynom für die Bedingungen: