Examenskurs - Grundsätzliches

Wie haben Sie alle Teiler der Zahl 12 ermittelt?
Vielleicht so, dass Sie alle natürlichen Zahlen

zwischen 1 und 12 daraufhin getestet haben, ob 12 durch

ohne Rest teilbar ist.
Dieses Verfahren mag für kleine Zahlen akzeptabel sein, führt aber langfristig zu großem Rechenaufwand, den man sich nicht mehr leisten kann oder will.
Eine geschickte Möglichkeit, alle Teiler zu bestimmen, besteht darin, zunächst alle Primteiler zu bestimmen, d.h. diejenigen Teiler zu finden, die selber Primzahlen sind.
Wir verwenden die Ergebnisse unserer Tabelle und stellen fest, dass zwischen 1 und 12 genau fünf verschiedene Primzahlen existieren: 2; 3; 5; 7; 11.
Nur die Primzahlen 2 und 3 sind auch Teiler von 12 und wir können die Zahl 12 in ihrer sogenannten Primzahlfaktorisierung schreiben:

Wir erkennen, dass jeder Teiler von 12 die gleichen Primteiler wie 12 hat, wobei nicht alle Primteiler von 12 auch echt in enthalten sein müssen.
Jeder Teiler von 12 hat also die Gestalt: , wobei der Exponent eine der Zahlen 0; 1 oder 2 und der Exponent eine der Zahlen 0 oder 1 ist.
Durch die möglichen Kombinationen ergeben sich verschiedene Teiler von 12.

		Wie haben Sie alle Teiler der Zahl 12 ermittelt? Vielleicht so, dass Sie alle natürlichen Zahlen zwischen 1 und 12 daraufhin getestet haben, ob 12 durch ohne Rest teilbar ist. Dieses Verfahren mag für kleine Zahlen akzeptabel sein, führt aber langfristig zu großem Rechenaufwand, den man sich nicht mehr leisten kann oder will. Eine geschickte Möglichkeit, alle Teiler zu bestimmen, besteht darin, zunächst alle Primteiler zu bestimmen, d.h. diejenigen Teiler zu finden, die selber Primzahlen sind. Wir verwenden die Ergebnisse unserer Tabelle und stellen fest, dass zwischen 1 und 12 genau fünf verschiedene Primzahlen existieren: 2; 3; 5; 7; 11. Nur die Primzahlen 2 und 3 sind auch Teiler von 12 und wir können die Zahl 12 in ihrer sogenannten Primzahlfaktorisierung schreiben: Wir erkennen, dass jeder Teiler von 12 die gleichen Primteiler wie 12 hat, wobei nicht alle Primteiler von 12 auch echt in enthalten sein müssen. Jeder Teiler von 12 hat also die Gestalt: , wobei der Exponent eine der Zahlen 0; 1 oder 2 und der Exponent eine der Zahlen 0 oder 1 ist. Durch die möglichen Kombinationen ergeben sich verschiedene Teiler von 12.
		Präsenzaufgabe: Wiederholen und beschreiben Sie die Überlegungen analog am Beispiel der Zahl 1225.		Lösung
		Diese Überlegungen anhand der konkreten Zahl 12 lassen sich verallgemeinern für jede natürliche Zahl . Mit Methoden der Algebra lässt sich beweisen, dass jede natürliche Zahl bis auf Reihenfolge eindeutig darstellbar ist als Produkt von Primzahlpotenzen: (alle sind Primzahlen und alle Exponenten sind natürliche Zahlen oder die Zahl 0). Will man absolute Eindeutigkeit der Darstellung erzwingen, so fordert man zusätzlich
		Präsenzaufgabe: Schreiben Sie die Zahlen 2000, 2001, 2002 in ihrer Primzahlfaktorisierung und bestimmen Sie dadurch die Teiler und die Anzahl der Teiler dieser Zahlen!		Lösung
		Mathematisch sinnvoll ist es, im Anschluss an eine Definition weiterführende Fragen zu stellen, die sich mit quantitativen oder qualitativen Aspekten im Umfeld des jeweiligen Begriffes beschäftigen. Je mehr Fragen man stellen kann, um so reichhaltiger wird die zugehörige Theorie werden, um so spannender vielleicht die erreichten Aussagen und Beweise. Die „richtigen“ Fragen zu stellen, ist eine Kunst für sich und muss eigens geübt werden. Oft kann man einen großen Satz der Mathematik erst dann würdigen, wenn man die dahinterliegende Fragestellung erkannt hat. Mögliche Fragen zur Definition des Teilers sind: Welche Teiler hat eine natürliche Zahl 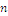im Allgemeinen? Wie viele Teiler hat eine natürliche Zahl 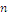im Allgemeinen? Gibt es ein (gutes, schnelles, handliches,…) Verfahren, um Teiler von 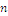zu berechnen? Welches 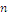hat wenige/viele Teiler? Welches 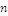hat genau 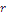verschiedene Teiler? 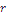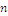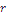Gibt es eine natürliche Zahl , so dass keine natürliche Zahl genau verschiedene Teiler hat? Wie kann man schnell herausfinden, ob eine Zahl durch 2 (bzw. 3; 4; 5; …) teilbar ist? Wie viele Primzahlen gibt es zwischen 1 und 100? Gibt es eine größte Primzahl oder kann man zu jeder noch so großen Primzahl eine noch größere finden? Bei dem Versuch, die ein oder andere Frage zu klären, wird man neue Begriffe und Notationen einführen, um möglichst präzise und allgemein verständlich Antworten formulieren zu können.