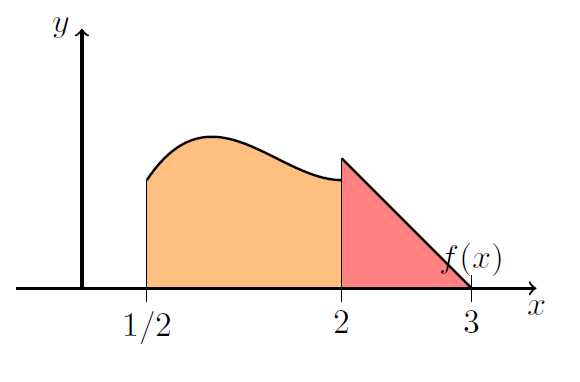Stückweise definierte Funktionen
So wie sich Flächeninhalte in der Geometrie aus einzelnen Stücken zusammensetzen lassen, ist dies auch beim Integrieren möglich. Dies ist besonders nützlich bei nicht-stetigen Funktionen, also Funktionen mit "Sprungstellen."
Beispiel 1.
\[f(x) = \begin{cases} \frac23x^3 + 3x^2 + 4x, & 1 \leq x < 2 \\ -x+3, & 2 \leq x \leq 3 \\ \end{cases} \]
Diese Funktion ist stückweise stetig und integrierbar. Für die praktische Rechnung bietet es sich an, die Funktion stückweise mit Hilfe des Hauptsatzes zu integrieren. Das heißt, es gilt:
\[\begin{aligned}\int\limits_{\frac12}^3 f(x)\, \mathrm d x &= \int\limits_{\frac12}^2 \frac23x^3 + 3x^2 + 4x\,\mathrm d x + \int\limits_2^3 -x+3\,\mathrm d x\\ &= \left[\frac16x^4+x^3+2x^2\right]_{x= \frac12}^{x=2} + \left[-\frac12x^2+3x\right]_{x=2}^{x=3}\\ &= \frac{577}{32}+\frac12 = \frac{593}{32}\end{aligned}\]Allgemein gilt für \(a < b < c \):
\[\int\limits_a^c f(x)\, \mathrm d x = \int\limits_a^b f(x)\, \mathrm d x + \int\limits_b^c f(x)\, \mathrm d x.\]
Gegeben sei eine stückweise definierte Funktion
\[ f(x):= \begin{cases}f_1(x)‚ & x\leqslant x_1, \\ f_2(x)‚ & x_1< x\leqslant x_2‚\\ f_3(x), & x> x_2.\end{cases}\]
In den Punkten \(x_1\) und \(x_2\) muss die Funktion nicht stetig sein, aber auf den Intervallen \( (-\infty‚x_1]\)‚ \( (x_1 ‚x_2]\) und \( (x_2‚\infty)\) sei
die Funktion integrierbar. Für die Funktion \[F(x):=\int_a^xf(\tau)\mathrm{d}\tau\]
mit \(a < x_1\) ergibt sich die Darstellung:
\[F(x) = c +\begin{cases}\int_a^xf_1(\tau)\,\mathrm{d}\tau‚ & x\leqslant x_1, \\ \int_a^{x_1}f_1(\tau)\,\mathrm{d}\tau+\int_{x_1}^xf_2(\tau)\,\mathrm{d}\tau‚ & x_1< x\leqslant x_2‚\\ \int_a^{x_1}f_1(\tau)\,\mathrm{d}\tau+\int_{x_1}^{x_2}f_2(\tau)\,\mathrm{d}\tau+\int_{x_2}^{x}f_3(\tau)\,\mathrm{d}\tau, & x> x_2.\end{cases}\]
mit \(c\in \mathbb{R}\). Dieses Schema lässt sich für Funktionen, die auf endlich vielen Intervallen stückweise definiert sind, übertragen.