Mit Hilfe der Definition lässt sich eine Ableitungsregel für Funktionen \(f\) herleiten, die Produkt einer Funktion \(u\) mit einem konstanten Faktor \(k\in\mathbb{R}\) sind:
\[f(x) = k\cdot u(x)\]
Wir betrachten dazu den Differentialquotienten an einer beliebigen Stelle \(x_0\).
\[\begin{align*} f'(x_0) &= \lim\limits_{x \to x_0} \frac{ f(x) - f(x_0)}{x - x_0} \\ &= \lim\limits_{x \to x_0} \frac{ku(x) - ku(x_0)}{x - x_0} = \lim\limits_{x \to x_0} \frac{ k\cdot (u(x) - u(x_0))}{x - x_0} \\ &= k\cdot \lim\limits_{x \to x_0} \frac{u(x) - u(x_0)}{x - x_0} = k\cdot u'(x_0) \end{align*}\]

Dabei wurde verwendet, dass:
\[ \lim\limits_{x \to x_0} {k\cdot g(x)} = k\cdot \lim\limits_{x \to x_0} g(x) \]

Ist \(u\) eine differenzierbare Funktion und \(k\in\mathbb{R}\) konstant, so gilt:
\[ f(x)=k\cdot u(x) \Rightarrow f'(x)=k\cdot u'(x) \]
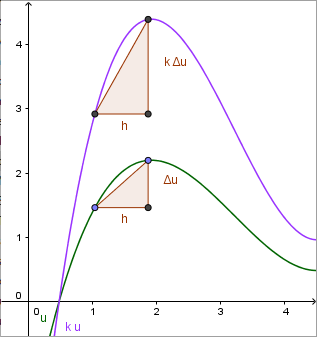
Anschaulich lässt sich diese Regel durch eine Streckung des Steigungsdreiecks verdeutlichen: