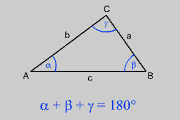Innenwinkelsumme des Dreiecks

  

Film

 
       
 
Satz:
  
   

Die Summe der Innenwinkel im Dreieck beträgt 180°.

a + ß + ? = 180°

  
       
   
Wenn- Dann- Formulierung:
 
    Wenn a, ß und ? die Innenwinkel eines Dreiecks sind, dann beträgt ihre Summe 180°.  
       
   
Voraussetzung:
  
    a, ß und ? sind die Innenwinkel eines Dreiecks.  
       
   
Behauptung:
  
    a + ß + ? = 180°  
         
   
Beweisidee:
    
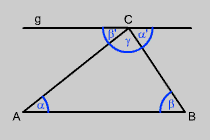
    Man zeichnet eine Parallele zu einer Seite durch den dieser Seite gegenüberliegenden Eckpunkt. Mit Hilfe des Satzes über Wechselwinkel beweist man den Satz.    
         
   
Beweis:
    
   
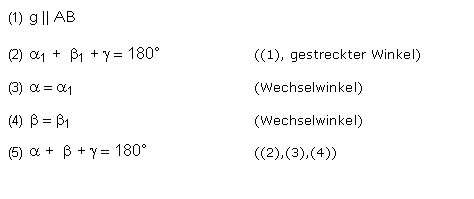
Bitte beachten Sie, dass α1 und α' (vgl. Bild) gleichzusetzen sind. Analog ist mit β vorzugehen.
         
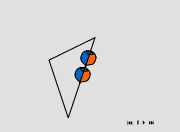
  Experimentelle Bestimmung der Winkelsumme im Dreieck
         
    Die Winkelsumme im Dreieck wird durch Messung der Innenwinkel ermittelt.    
         
    Bitte schalten Sie Java ein, um eine Cinderella-Konstruktion zu sehen.  

Ziehen Sie das Dreieck in verschiedene Lagen und addieren Sie die Meßwerte der drei Innenwinkel!

Was fällt auf?